WPP #9: Unit L Concepts 4-8 - FCP, Combinations, and Permutations

Create your own Playlist on MentorMob!

SP #6: Unit K Concept 10 - Writing a Repeating Decimal as a Rational Number Using Geometric Series

        Concerning this problem, one in which you are tasked with finding the fraction of a number with repeating decimals, there are not really many things one has to remember to do. Though, it is a bit important that one remember to add whatever you didn't account for in your geometric series. In my case, it was the 4, since it was not part of the repeating numbers. You must also remember to plug your answer back in, to see whether or not you did it correctly. I mean, you don't really have to, but it is quite useful for saving a bit of face when having your problem examined by your colleagues. Yep.

Fibonacci Haiku: Stars

Stars

Dream

All alone

Yet inside dreams

The brightness of the stars
Invites me and you to dance with them

http://thecajunsamurai.files.wordpress.com/2012/05/5centimeterspersecond-5.jpg
Movie: 5 Centimeters Per Second

SP #5: Unit J Concept 6 - Partial Fraction Decomposition with Repeated Factors

        First of all, we must remember that what distinguishes these types of problems from other ones is that they have repeated factors. Basically, all you do is count up, which means, as you separate the initial fraction, you repeat the factors, but with their exponent increasing incrementally by 1. It sounds confusing, but if you had saw an example, you'd get it right away. As always, with these types of lengthy problems, you must remember to calculate carefully, as one mistake could ruin you. Oh, and you can't use calculators for many of these problems, since most of the answers come out as decimals, which we are not permitted to utilize, unless they are definite (don't go on forever). Fin.

SP #4: Unit J Concept 5 - Partial Fraction Decomposition with Distinct Factors

        There are several crucial things that one must remember in order to fully get through this struggle and emerge victorious. First of all, one must pay close attention to the calculations that they do in their head, because it's really easy to mess up. And if you mess up once during the problem, you'll have to go back and redo the entire thing from that point onward. Second of all, you have to remember to transfer the correct sign (+/-), and also utilize them correctly, for the next step. One mistake could mess up your entire problem. Lastly, if you're not utilizing a calculator to derive RREF (Reduced Row Echelon Form), you have to remember to utilize your elementary row operations without mistake, for one mistake could, again, cost you the entire answer, ergo, a whole lot of time. That is all.

SV #5: Unit J Concept 3 - Gaussian Elimination

        The first and foremost important thing to remember to do, is distinguish which rows and numbers you need to work on, and which rows you may use in order to eliminate the numbers. It's really the entire backbone of this concept. Another important thing to remember to do is to calculate correctly, for if you mess up even once, you will proceed to arrive at a wrong answer. Lastly, you should check your answers with a calculator, if an answer sheet is not readily available. That is all.

WPP #6: Unit I Concepts 3-5 - Compound Interest

Create your own Playlist on MentorMob!

SV #4: Unit I Concept 2 - Graphing Logarithmic Equations

        Some important things that need to be noted whilst completing problems of this particular field of study, are: remembering how these types of problems share the same structure, remembering how you find the asymptotes for logarithmic equations, and remembering the domain/range of logarithmic equations. First of all, the parent type function for these problems  is log base b of (x minus h) plus k. Second of all, the asymptotes for logarithmic equations will always be x = h, and you can remember this specific rule with the phrase "The Log's Xylophone was Happy and Rich", where you derive x = h from "Xylophone was Happy". Lastly, the domain of logarithmic equations will always be restricted (unless there's no h value), and their ranges will never be restricted. This can also be remembered by the previously noted phrase, and is extracted from "Rich", in which the r proclaims that the range is to never be restricted. The end.

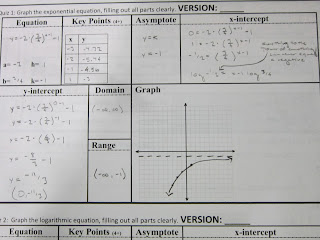
SP #3: Unit I Concept 1 - Graphing Exponential Equations

        Alright, so some important things to remember when finding the components of exponential equations, and afterwards, graphing it, include: making sure that you have extracted the a, b, h, and k values correctly, making sure that you've got the right type of asymptote for the such equations, and remembering how to tell whether or not the equation will have an x-intercept or not. Basically, you just adhere to the parent graph closely (adapted for the exponential equations) to make sense of said values. The exponential yak died will tell you that exponential equations have the asymptotes of y = k. It will also tell you that the domain is never restricted, which is why y-intercepts will always be present in these equations. Lastly, you can easily tell whether or not an equation has an x-intercept by seeing whether or not the equation crosses the x-axis, which would only occur when the horizontal asymptote is not blocking the way to the axis.

SV #3: Unit H Concept 7 - Expanding Logarithms

        Some important things you must pay attention to are how you synthesize logarithms from factors of big numbers, and remembering to substitute in the variables. Also, you must remember to utilize the properties of logs in order to formulate more logarithms that you may be required to utilize in order to get to the desired endpoint. Another somewhat important thing to remember to do is to turn the denominator log into subtraction. Lastly, if none of the given clues can fit in, you may be able to multiply the endpoint in order to factor the number. Either that, or you're wrong. Anyways, the end.

SV #2: Unit G Concepts 1-7 - Finding All Parts and Graphing A Rational Function

        This problem elaborates upon rational functions, and (kind-of) how to graph them. In just this one problem, we utilize many different concepts, such as factoring and all that, yet the foremost important things, however, are to remember what to do to find asymptotes/points. And all of that, we have committed to memory, through DIVAH. Anyways, to find the intercepts and all, we just have to remember to set the other value to 0. Graphing is pretty easy, as all you really do is make the values that head on to infinity, slowly approach the asymptotes (basically, you just make something nearly parallel to the asymptotes).
        Some special things that you need to remember are what to do to find stuff, how to graph, and how to put all of this into your calculator to make it easier and or check. Anyways, you always have either a horizontal asymptote (ratio for same degree on top and bottom, y = 0 for degree being bigger on bottom), a slant asymptote (when the top degree is bigger by 1, y equals the numerator divided by the denominator, leaving out the remainder), or none (when the top degree is bigger by more than 1). To graph, all you do is just kind-of make lines parallel to the asymptotes, and that will reach infinity on some value. To put all of this into your calculator, you might have to just do it. That is all.

SV #1: Unit F Concept 10 - Finding All Real and Imaginary Zeroes of A Polynomial

        This problem concerns deriving zeroes from given polynomials of either the 4th or 5th degree. Basically, you work out the problem until you arrive at an end result of 4 zeroes (for 4th degree polynomials), or 5 zeroes (for 5th degree polynomials). In doing so, however, there are several crucial steps that must be taken in order to ensure the success of your efforts. Anyways, this could be useful in graphing, too.
       Some important things that one must pay attention about in order to master this concept include remembering to use the rational roots theorem, and the Descartes Rule of Signs, and remembering to put zeroes in to fill voids when an x is missing in the polynomial. The most important thing, however, is to remember that you may more easily complete this process by utilizing a graphing calculator in order to identify zero heroes. But, as scholars, is it not more honorable to walk the path filled with thorns in order to ensure our complete mastery of this concept? Either way, yeah; it is easier to use the graphing calculator.

SP #2: Unit E Concept 7 - Graphing A Polynomial And Identifying All Key Parts

        The purpose of this problem is to derive a polynomial function from a designated number of zeros and a designated power and coefficient. With this in mind, we graph a fourth degree polynomial with an even coefficient for its highest x-power, all without of the complications that a graphing calculator obviously presents. This is done by first extracting the factors from the polynomial, or formulating them from the zeros that were given, and then deciding the orientation of the ends of the graph. That is all.
        Some important facts to factor in are to pay attention to the: orientation, through / bounce / curve x-intercepts, and whether or not it looks right. An important thing that must be done (that is excluded from this problem) in order to graph a more accurate graph, is to try and figure out the extrema of the graph. Don't forget to utilize that, and of course, the y-intercept in more accurately displaying your graph. An extra thing that could be done would be to check whether or not your graph is correct on a graphing calculator. Don't forget to input the correct things though, for your calculator is only as smart as you.

WPP #4: Unit E Concept 3 - Maximizing Area

Create your own Playlist on MentorMob!

WPP #3: Unit E Concept 2 - Path of A Leap

Create your own Playlist on MentorMob!

SP #1: Unit E Concept 1 - Graphing A Quadratic and Identifying All Key Parts

        This problem is about deriving a parent function type equation from a regular trinomials, so that graphing the equation wouldn't be as hard as it would have been had you tried to graph the other way. Basically, it's about finding the values that we deem crucial in graphing polynomials, which include the vertex, x-intercept(s) (if there are any), the y-intercept (if there is one), and the axis of symmetry. Ultimately, it's about going through this infinitude of steps, and arriving at a simpler means.

        I think that the reader needs most, to pay special attention to whether or not my writing is intelligible to them or not. However, in all seriousness, though, I think that they need to know that all of the important values that we need, can be calculated simply on a calculator right from the start, without having to go through any of these steps. To each, their own, I guess. Also, it's pretty important that you realize imaginary numbers cannot be graphed regularly, such as regular x-values, on a regular graph.

WWP #2: Unit A Concept 7 - Profit, Revenue, Cost

Create your own Playlist on MentorMob!

WWP #1: Unit A Concept 6 - Linear Models

Create your own Playlist on MentorMob!