WPP #6: Unit I Concepts 3-5 - Compound Interest

Create your own Playlist on MentorMob!

SV #4: Unit I Concept 2 - Graphing Logarithmic Equations

        Some important things that need to be noted whilst completing problems of this particular field of study, are: remembering how these types of problems share the same structure, remembering how you find the asymptotes for logarithmic equations, and remembering the domain/range of logarithmic equations. First of all, the parent type function for these problems  is log base b of (x minus h) plus k. Second of all, the asymptotes for logarithmic equations will always be x = h, and you can remember this specific rule with the phrase "The Log's Xylophone was Happy and Rich", where you derive x = h from "Xylophone was Happy". Lastly, the domain of logarithmic equations will always be restricted (unless there's no h value), and their ranges will never be restricted. This can also be remembered by the previously noted phrase, and is extracted from "Rich", in which the r proclaims that the range is to never be restricted. The end.

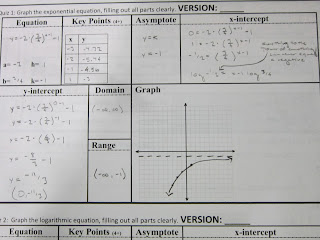
SP #3: Unit I Concept 1 - Graphing Exponential Equations

        Alright, so some important things to remember when finding the components of exponential equations, and afterwards, graphing it, include: making sure that you have extracted the a, b, h, and k values correctly, making sure that you've got the right type of asymptote for the such equations, and remembering how to tell whether or not the equation will have an x-intercept or not. Basically, you just adhere to the parent graph closely (adapted for the exponential equations) to make sense of said values. The exponential yak died will tell you that exponential equations have the asymptotes of y = k. It will also tell you that the domain is never restricted, which is why y-intercepts will always be present in these equations. Lastly, you can easily tell whether or not an equation has an x-intercept by seeing whether or not the equation crosses the x-axis, which would only occur when the horizontal asymptote is not blocking the way to the axis.

SV #3: Unit H Concept 7 - Expanding Logarithms

        Some important things you must pay attention to are how you synthesize logarithms from factors of big numbers, and remembering to substitute in the variables. Also, you must remember to utilize the properties of logs in order to formulate more logarithms that you may be required to utilize in order to get to the desired endpoint. Another somewhat important thing to remember to do is to turn the denominator log into subtraction. Lastly, if none of the given clues can fit in, you may be able to multiply the endpoint in order to factor the number. Either that, or you're wrong. Anyways, the end.

SV #2: Unit G Concepts 1-7 - Finding All Parts and Graphing A Rational Function

        This problem elaborates upon rational functions, and (kind-of) how to graph them. In just this one problem, we utilize many different concepts, such as factoring and all that, yet the foremost important things, however, are to remember what to do to find asymptotes/points. And all of that, we have committed to memory, through DIVAH. Anyways, to find the intercepts and all, we just have to remember to set the other value to 0. Graphing is pretty easy, as all you really do is make the values that head on to infinity, slowly approach the asymptotes (basically, you just make something nearly parallel to the asymptotes).
        Some special things that you need to remember are what to do to find stuff, how to graph, and how to put all of this into your calculator to make it easier and or check. Anyways, you always have either a horizontal asymptote (ratio for same degree on top and bottom, y = 0 for degree being bigger on bottom), a slant asymptote (when the top degree is bigger by 1, y equals the numerator divided by the denominator, leaving out the remainder), or none (when the top degree is bigger by more than 1). To graph, all you do is just kind-of make lines parallel to the asymptotes, and that will reach infinity on some value. To put all of this into your calculator, you might have to just do it. That is all.