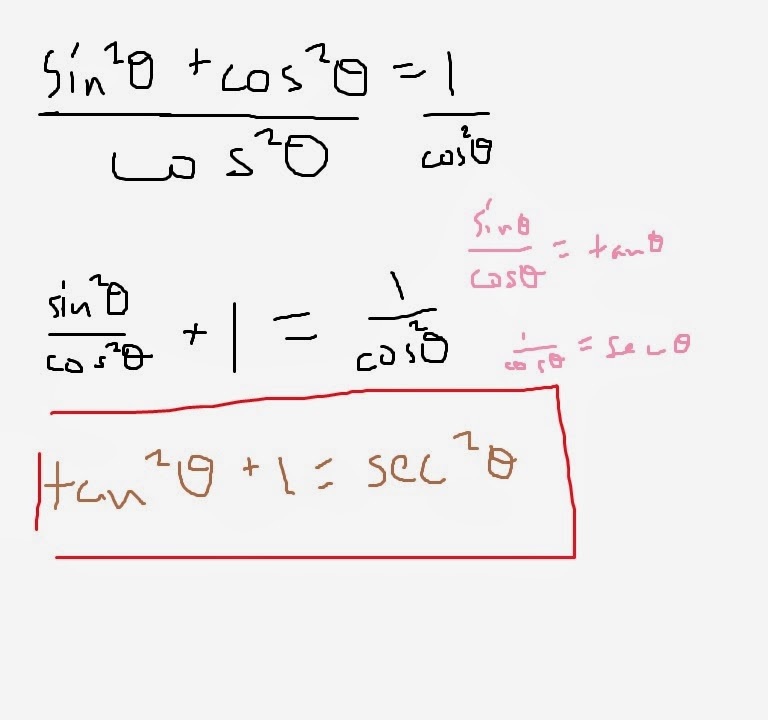SP #7: Unit Q Concept 2 - Finding All Trigonometric Functions Using Identities

This SP #7 was made in collaboration with Sergio Sanchez. Please visit the other awesome posts on their blog by going here.

Our given is:

One of the first and foremost steps that must be undertaken, is identifying which quadrant we are working with. Although, using the values of the trig functions and their accompanied signs would do just as well.

Next, we'd just go right into solving this with trigonometric identities. It's pretty self-explanatory had one taken this course. But, for the sake of something: first, I list out the identity, and then, substitute in the value(s) that I already have. I then solve it until there is one unknown trigonometric function is on one side, and a value is on the other.

As for Sergio's work, I suppose that I shall put forth some sort of explanation, in lieu of the original creator, who just gave me this picture. Basically, he plugged in values that were given (from the tangent trigonometric function), into the Pythagorean Theorem, in order to get the excluded side's value. Having gotten all of the sides, he just plugged them into the rest of the unknown trigonometric functions.

It is important that one remembers what all of the trigonometric functions mean - what sides they represent, and how they represent each other. As in, you have to remember that sine is opposite / hypotenuse, and also, 1 / secant. This is important because if you could fail pretty easily if you use the wrong functions/identities. It's also very important for one to remember to rationalize (which I did), and reduce (which I didn't do). Apparently, it's the most important thing you could do for yourself, for forgetting to do so, would result in loss of points on your tests or whatever.

I/D #3: Unit Q - Pythagorean Identities

Inquiry Activity Summary:

1) sin² θ + cos² θ = 1
According to some higher truth, this is true - so, I guess that I'll do as I am told and prove this Pythagorean identity true, in terms of the Pythagorean Theorem and a unit circle. In terms of the unit circle, the Pythagorean Theorem would be x² + y² = r². Since we want 1 on one side, we should divide both sides by r², which would leave us with (x/r)² + (y/r)² = 1. In the unit circle, the ratio of x/r is sine, and the ratio of y/r is cosine. So, if we substitute that in, we get sin² θ + cos² θ = 1.

2) The Two Other Ones
What you would basically do, is divide both sides by either trigonometric function, in order to create ratios that would equal other trigonometric functions. Meaning: you create different ratios by making either sine or cosine equal to 1.

Inquiry Activity Reflection:

1) "The connections I see so far between Units N, O, P, and Q so far are" that they all work together - the unit circle, angles, trigonometric functions, all that stuff - in order to make our experience in math class harder. They all made us critically think about what we are given, and helped us put the pieces of this conundrum together.

2) "If I had to describe trigonometry in THREE words, they would be": "Gotta go fast."

WPP #13/14: Unit P Concepts 6-7 - The Laws of Sine and Cosine

This WPP13-14 was made in collaboration with Sergio Sanchez.  Please visit the other awesome posts on their blog by going here.

Sergio's Problem
Mark arrives at a rather tall building with the rest of his band (to sign a record deal). He is standing 50 feet away from the building, when he looks up, and sees a large He-man banner hanging from one of the windows, and thinks to himself: "Well, would you look at that." If the angle of elevation to the top of the building is N 45° W degrees, and the angle of elevation to the poster is N 25° W degrees, at what height is the banner hung?

[TV Movie Poster]

Our first step in solving this, would be to figure out that the height of the wall is of no relevance - Sergio's fault - yet still, draw a picture of it.

Our next step would be to include the poster and label our given values (50 feet and 25°), and from there, calculate the other angle, since Sergio had decided to simplify our lives and make this a right triangle, which would leave the other angle as 65°.

Lastly, we would utilize the Law of Sines in order to match up 65° with 50, and make sin 65° / 50 equal to sin 25° / x, which, cross-multiplied and simplified, would lead to 23.3 feet as the height of the poster.

Brian's Problem
He-Man smiles upon his admirers, and although he was just a a guy on a poster, his bright smile reflects the sunlight, and shines the radiance upon Mark and the rest of his band. Somehow, he finds that the angle from which He-Man's smile shined light upon his buddies and him, was 115° (navigation method), and that the lengths that had sandwiched that angle, were 35 feet and 25 feet. What length of area did that light cover?


Our first step would be to draw our triangle and label all of the parts, in order to help us organize our next actions.

Our next and last step, would be to plug in all of our values into the Law of Cosines, simplify, and find our answer.

BQ #1: Unit P Concepts 1-5: Non-right Triangle Trigonometry

1. Law of Sines: The Law of Sines is indispensable in sustaining our cushy, privileged lives, because it maintains the space-time continuum in our universe, and because you need it in order to solve for all of the values of any triangle that exists. Of course, you could use the Pythagorean Theorem and other simpler trigonometric functions - but only for right triangles, though, for some apparent reason.

We could prove this law by utilizing our previous knowledge of trigonometry, by creating a line perpendicular to side b and touching the vertex of angle B in a non-right triangle. We shall label this side, h, for the sake of convenience for something else we shall do in just a moment.

Now, we have something that we can work with - two right triangles. And, if we use trigonometry, we will be able to prove the Law of Sines using our prior knowledge. Basically, sine of A, would be h/c, and sine of C, would be h/a. If we multiply both sides of sin A = h/c by c, then h = sin A x c. And if we multiply both sides of sin C = h/a, then h = sin C x a.

With h being equal and all, we will be able to set them equal to each other. This makes sin A x c = sin C x a. If we divide both sides by c x a, then sin A / a = sin C / c, which proves the Law of Sines (or at least 2/3 of it). Just kidding. Since we only use two at a time (you couldn't possibly have = twice in an equation, right?), all we would have to do is switch around the letters, and everything would be fine.

4. Area of An Oblique Triangle: The area of any triangle should be 1/2 b x h (b is base, which would be the side of b anyways, and A, area in this case), which roughly translates to: half of double of the triangle. We would use it normally for our immediate needs - but, we lack the value of h, which can be substantiated, by trigonometry. Of course, this only occurs when we don't have the value of h, but do have, or can get the values of, the rest of the triangle.

So, we can utilize trigonometry, to get h, starting with the fact that sin C = h / a. If we multiply both sides by a, then h = sin C x a. And, if we substitute that into the equation for the area of a triangle, as the value of h, then it'd simply be A = 1/2 b x (sin C x a).

This is related to the area formula that we are familiar with, because it is the area formula that we are familiar with - the only thing changed, is that h is a different value. Lastly, these letter can change around a bit, as such:

[Math Is Fun]

Works Cited: Math Is Fun

WPP #12: Unit O Concept 10 - Angles of Elevation and Depression

[cdn.screenrant.com/wp-content/uploads/He-Man-Masters-of-the-Universe-Movie.jpeg]

He-Man and his comrades are heading towards the battlefield, in a planned face-off against Skeletor and his goons. When they confronted their enemies, they had found an unfortunate situation: Skeletor's forces were on higher ground than them (on a mountain), leading to a widely unfair advantage. He-Man thought out the situation while his comrades kept the enemy busy, and had decided to calculate whether or not throwing a projectile at Skeletor was practical or not. He had estimated about 200 feet of distance between them (from He-Man to the base of the mountain), and a 70° angle of elevation to Skeletor. How far would his throw have to be, in order for his projectile to (diagonally and in a straight line) reach Skeletor?

  S(keletor)

   |\

   |  \

   |    \                                  cos 70° = 200 ft.

   |      \                                                    h

   |        \

   |          \                                  h x cos 70° = 200 ft.

   |            \

   |              \                                     200 ft.

   |                \                                  --------- = 584.76 ft.

   |                  \                                cos 70°

   |             70° \ H(e-Man)

         200 ft.

Seeing as how a throw that would have to travel 584.76 ft. was impractical, He-Man had simply decided to find a nearby mountain with a higher elevation, in order to reduce the required power in that throw. After a short while, He-Man finds a fitting spot upon a mountain, measuring 600 ft. in height. If Skeletor's elevation was 549.5 ft., and the angle of depression was 10°, then what would be the distance that He-Man's new-and-improved throw have to be?

I/D #2: Unit O - How Can We Derive the Patterns For Our Special Right Triangles?

1) We may derive a 30/60/90 degree triangle's special pattern from an equilateral triangle with a side length of 1, by first dividing the triangle into two halves that are completely equal. You'd split it right in the middle, creating two triangles that share one side of the previously whole equilateral triangle (which equaled 1), and the side that was created by splitting them in half. They each have their own side of 1, across from the 90° angle that they both have, which was created by the division.

Since we divided the side which had previously equaled 1 into two equal parts, then each triangle must have a side of 1/2. So, if we proceed with that deduction, then that side, squared, added with the other side that's not the hypotenuse, squared, should equal the hypotenuse, squared. Basically, a² + b² = c² (Pythagorean Theorem), with 1/2 being a, the other leg being b, and 1 being c. This works because the triangles we had created, have 90° angles, and therefore, have an assumed hypotenuse across from them, along with the values for a and b that fit into the aforementioned equation. (1/2)² + b² = (1)² would be 1/4 + b² = 1, and subtracting 1/4 from both sides would result in 3/4 as the value for b². And, if we take the square root of the entire fraction, then it should equal √3/√4, which would reduce into √3/2.

Lastly, we'd have to save this extremely rare knowledge, by multiplying everything by 2, and then, by a variable, so that this pattern will be easily transferable to any 30/60/90 degree triangle. Multiplying each side by 2n, basically, would yield a hypotenuse of 2n, a value of n for the side across from the 30° angle, and a value of n√3 for the side across from the 60° angle. This pattern shall forever exist for any 30/60/90 degree triangle, since the pattern was derived from ratios that will be the same for all 30/60/90 degree triangles.

2) We may derive a 45/45/90 degree triangle's special pattern from a square with the equal sides of 1, by diagonally dividing two 90° angles (across from each other) exactly in half, and making four 45° angles - two for each triangle. Each triangle would then, each have two sides that equal 1, and share a hypotenuse.

So, since the two triangles that we have given life to have 90° angles, then the Pythagorean Theorem can be utilized in order to find the length of the hypotenuse in this set-up. 1² + 1² = c² shall become c² = 2, and from that point onward, be √2.

In order to again, preserve our newly-discovered and revolutionary (in the field of mathematics) pattern, we must multiply all of our triangles' values by n, in order to create a distinct pattern that we can follow for any 45/45/90° triangle. Everything just basically gets an n attached to it.

Inquiry Activity Reflection
1) Something I never noticed before about special right triangles is that their established patterns can be deduced from a logical procedure, instead of just being "there", because we were told that it happened to be "there".

2) Being able to derive these patterns myself aids in my learning because I'm not just remembering given facts or something - I'm actually finding out this stuff myself.