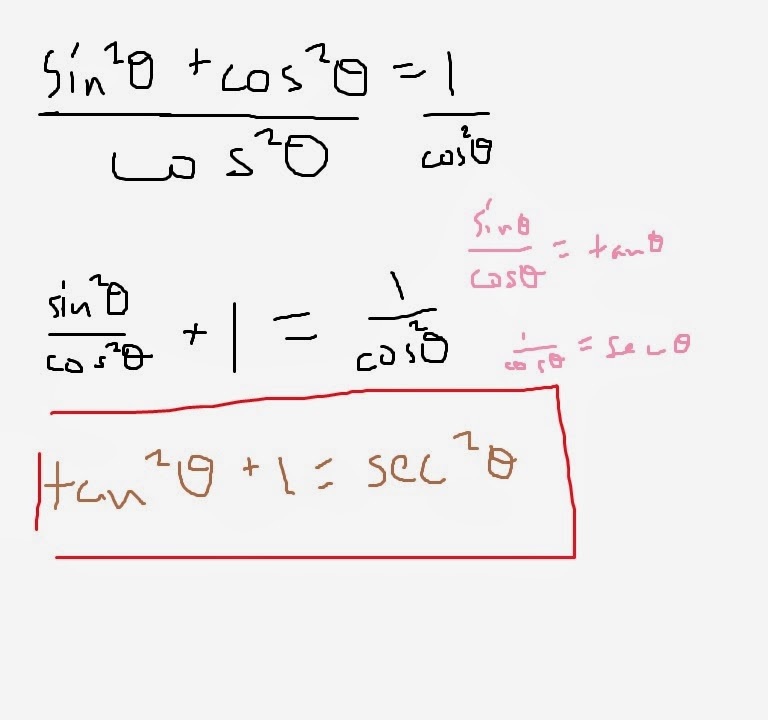1) sin² θ + cos² θ = 1
According to some higher truth, this is true - so, I guess that I'll do as I am told and prove this Pythagorean identity true, in terms of the Pythagorean Theorem and a unit circle. In terms of the unit circle, the Pythagorean Theorem would be x² + y² = r². Since we want 1 on one side, we should divide both sides by r², which would leave us with (x/r)² + (y/r)² = 1. In the unit circle, the ratio of x/r is sine, and the ratio of y/r is cosine. So, if we substitute that in, we get sin² θ + cos² θ = 1.
2) The Two Other Ones
What you would basically do, is divide both sides by either trigonometric function, in order to create ratios that would equal other trigonometric functions. Meaning: you create different ratios by making either sine or cosine equal to 1.
Inquiry Activity Reflection:
1) "The connections I see so far between Units N, O, P, and Q so far are" that they all work together - the unit circle, angles, trigonometric functions, all that stuff - in order to make our experience in math class harder. They all made us critically think about what we are given, and helped us put the pieces of this conundrum together.
2) "If I had to describe trigonometry in THREE words, they would be": "Gotta go fast."