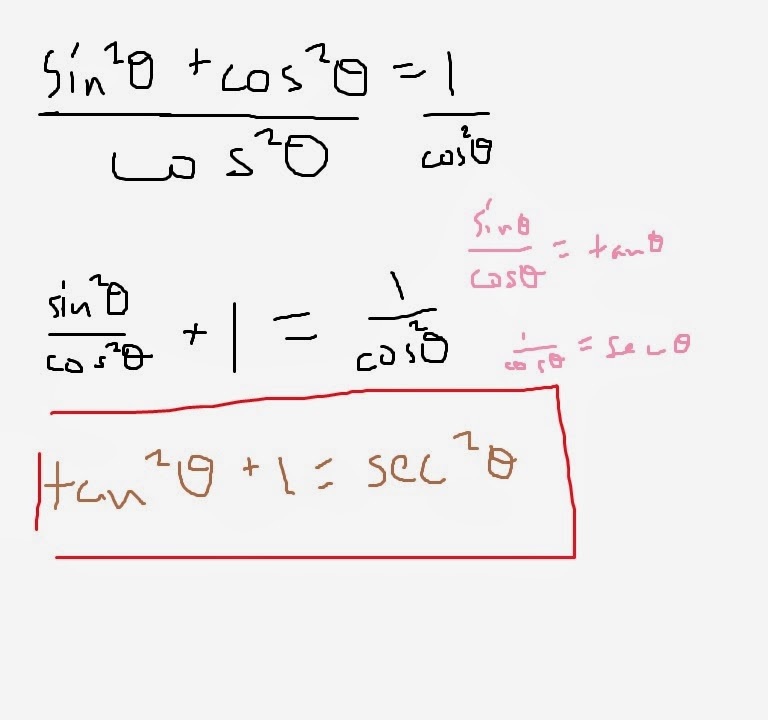BQ #5: Unit T Concepts 1-3

Why do sine and cosine NOT have asymptotes, but the other four trig graphs do? Use unit circle ratios to explain?
Sine and cosine do NOT have asymptotes, because their ratios on the unit circle are x (for cosine) and y (for sine), over r. And, r shall always be equal to 1, being the length of the radius of the circle. The logic behind that explaining how they don't have asymptotes, is that for there to be an asymptote, the denominator of a trigonometric function's ratio, has to be able to be equal to 0. Asymptotes only exist when there is a denominator that could possibly be equal to 0, therefore restricting a certain part of the graph. It is from that same requirement for there to be an asymptote, that we can reason that secant/cosecant/tangent/cotangent have asymptotes. Their ratios on the unit circle should be, respectively: r/x. r/y, y/x, and x/y. Since their denominators are not restricted towards being solely 1 as sine and cosine are, 0 is a possibility for the denominators. The end.

BQ #2: Unit T Intro

How do the trig graphs relate to the unit circle?
Trig graphs relate to the unit circle in how the unit circle can be utilized to find where a certain trig function is positive or negative on a graph. For example, sine is positive in the first and second quadrants - between 0° and 180°, or between 0 and π. If we utilize radians on our x-axis, and have some fraction of π as our markings, then we may isolate the area of the graph between 0 and π as the area in which sine would be positive. Finding these positive/negative areas works with every trigonometric function, though you would have to account for asymptotes as well for denominators that could possibly be equal to 0.

Period? 
Why is the period for sine and cosine 2π, whereas the period for tangent and cotangent is π?
The periods for sine and cosine are 2π because it takes a full rotation of the unit circle, which is 2π, for sine and cosine to fulfill the requirements to be periods. And, a period is a portion of any trig graph that is repeated over and over again without change. To illustrate this example, the values of sine, going through the unit circle's four different quadrants, should be +, +, -, -. Having anything less than those four repeating themselves would create inconsistency, so there you have it. On the other hand, the periods for tangent and cotangent are π because it takes half the rotation of the unit circle. π, for tangent and cotangent to continually repeat themselves consistently. The values of tangent/cotangent, going through the unit circle's four different quadrants, should be +, -, +, -. And having just two repeat themselves continually should be enough to constitute an acceptable pattern.

Amplitude?
How does the fact that sine and cosine have amplitudes of one (and the other trig functions don't have amplitudes) relate to what we know about the Unit Circle?
Sine and cosine have amplitudes, while the other trig functions don't have amplitudes, because their ranges are restricted by how both of their trigonometric ratios have 'r' as the sole value in their denominators. And, on the unit circle, 'r' is equal to 1, being the length of the radius. The other trig functions don't have amplitudes because restrictions such as 'r' aren't in their ratios.

Reflection #1: Unit Q - Verifying Trig Functions

1. Verifying a trigonometric function means simplifying it and or replacing it with other trigonometric functions so that it may equal a set value. You would multiply/divide/add/subtract numbers or some other mathematical asset in order to advance with the equation and simplify it, until it arrives at the value you want it too equal. You may also replace trigonometric functions with other trigonometric functions, such as making tangent into sine divided by cosine. Or, you could make sine squared added with cosine squared, equal 1. One should really try to work with all of the trigonometric identities in order to help them arrive at what they want. And, it will always (at least for what we're doing) be equal. You're not trying to prove it wrong or right - rather, you're showing the work that it takes in order to prove it right. So, if you ever find adversity, don't pass off the equation as invalid.

2. I have found all of the tips and tricks equally helpful. The best tip/trick that I believe anyone could get, is that all of the equations are valid, so you can't give up and write it off as not equal. The most fundamental, and necessary (for about each and every problem you'll have to solve) is tip/trick, is that you have to utilize identities. Unless, of course, you get the problem tangent plus 1 equals tangent plus 2 minus 1, which would then necessitate the question of whether or not you are doing the right problem.

3. Basically, I'd look at what I could do: subtract/multiply by conjugate/replace, and do it. If I end up at a dead end, I'd try again, until I'd get it. And if I don't get it again, I shall try again.

P.S. Not giving up is the fundamental thought process for success in Unit Q.

SP #7: Unit Q Concept 2 - Finding All Trigonometric Functions Using Identities

This SP #7 was made in collaboration with Sergio Sanchez. Please visit the other awesome posts on their blog by going here.

Our given is:

One of the first and foremost steps that must be undertaken, is identifying which quadrant we are working with. Although, using the values of the trig functions and their accompanied signs would do just as well.

Next, we'd just go right into solving this with trigonometric identities. It's pretty self-explanatory had one taken this course. But, for the sake of something: first, I list out the identity, and then, substitute in the value(s) that I already have. I then solve it until there is one unknown trigonometric function is on one side, and a value is on the other.

As for Sergio's work, I suppose that I shall put forth some sort of explanation, in lieu of the original creator, who just gave me this picture. Basically, he plugged in values that were given (from the tangent trigonometric function), into the Pythagorean Theorem, in order to get the excluded side's value. Having gotten all of the sides, he just plugged them into the rest of the unknown trigonometric functions.

It is important that one remembers what all of the trigonometric functions mean - what sides they represent, and how they represent each other. As in, you have to remember that sine is opposite / hypotenuse, and also, 1 / secant. This is important because if you could fail pretty easily if you use the wrong functions/identities. It's also very important for one to remember to rationalize (which I did), and reduce (which I didn't do). Apparently, it's the most important thing you could do for yourself, for forgetting to do so, would result in loss of points on your tests or whatever.

I/D #3: Unit Q - Pythagorean Identities

Inquiry Activity Summary:

1) sin² θ + cos² θ = 1
According to some higher truth, this is true - so, I guess that I'll do as I am told and prove this Pythagorean identity true, in terms of the Pythagorean Theorem and a unit circle. In terms of the unit circle, the Pythagorean Theorem would be x² + y² = r². Since we want 1 on one side, we should divide both sides by r², which would leave us with (x/r)² + (y/r)² = 1. In the unit circle, the ratio of x/r is sine, and the ratio of y/r is cosine. So, if we substitute that in, we get sin² θ + cos² θ = 1.

2) The Two Other Ones
What you would basically do, is divide both sides by either trigonometric function, in order to create ratios that would equal other trigonometric functions. Meaning: you create different ratios by making either sine or cosine equal to 1.

Inquiry Activity Reflection:

1) "The connections I see so far between Units N, O, P, and Q so far are" that they all work together - the unit circle, angles, trigonometric functions, all that stuff - in order to make our experience in math class harder. They all made us critically think about what we are given, and helped us put the pieces of this conundrum together.

2) "If I had to describe trigonometry in THREE words, they would be": "Gotta go fast."

WPP #13/14: Unit P Concepts 6-7 - The Laws of Sine and Cosine

This WPP13-14 was made in collaboration with Sergio Sanchez.  Please visit the other awesome posts on their blog by going here.

Sergio's Problem
Mark arrives at a rather tall building with the rest of his band (to sign a record deal). He is standing 50 feet away from the building, when he looks up, and sees a large He-man banner hanging from one of the windows, and thinks to himself: "Well, would you look at that." If the angle of elevation to the top of the building is N 45° W degrees, and the angle of elevation to the poster is N 25° W degrees, at what height is the banner hung?

[TV Movie Poster]

Our first step in solving this, would be to figure out that the height of the wall is of no relevance - Sergio's fault - yet still, draw a picture of it.

Our next step would be to include the poster and label our given values (50 feet and 25°), and from there, calculate the other angle, since Sergio had decided to simplify our lives and make this a right triangle, which would leave the other angle as 65°.

Lastly, we would utilize the Law of Sines in order to match up 65° with 50, and make sin 65° / 50 equal to sin 25° / x, which, cross-multiplied and simplified, would lead to 23.3 feet as the height of the poster.

Brian's Problem
He-Man smiles upon his admirers, and although he was just a a guy on a poster, his bright smile reflects the sunlight, and shines the radiance upon Mark and the rest of his band. Somehow, he finds that the angle from which He-Man's smile shined light upon his buddies and him, was 115° (navigation method), and that the lengths that had sandwiched that angle, were 35 feet and 25 feet. What length of area did that light cover?


Our first step would be to draw our triangle and label all of the parts, in order to help us organize our next actions.

Our next and last step, would be to plug in all of our values into the Law of Cosines, simplify, and find our answer.

BQ #1: Unit P Concepts 1-5: Non-right Triangle Trigonometry

1. Law of Sines: The Law of Sines is indispensable in sustaining our cushy, privileged lives, because it maintains the space-time continuum in our universe, and because you need it in order to solve for all of the values of any triangle that exists. Of course, you could use the Pythagorean Theorem and other simpler trigonometric functions - but only for right triangles, though, for some apparent reason.

We could prove this law by utilizing our previous knowledge of trigonometry, by creating a line perpendicular to side b and touching the vertex of angle B in a non-right triangle. We shall label this side, h, for the sake of convenience for something else we shall do in just a moment.

Now, we have something that we can work with - two right triangles. And, if we use trigonometry, we will be able to prove the Law of Sines using our prior knowledge. Basically, sine of A, would be h/c, and sine of C, would be h/a. If we multiply both sides of sin A = h/c by c, then h = sin A x c. And if we multiply both sides of sin C = h/a, then h = sin C x a.

With h being equal and all, we will be able to set them equal to each other. This makes sin A x c = sin C x a. If we divide both sides by c x a, then sin A / a = sin C / c, which proves the Law of Sines (or at least 2/3 of it). Just kidding. Since we only use two at a time (you couldn't possibly have = twice in an equation, right?), all we would have to do is switch around the letters, and everything would be fine.

4. Area of An Oblique Triangle: The area of any triangle should be 1/2 b x h (b is base, which would be the side of b anyways, and A, area in this case), which roughly translates to: half of double of the triangle. We would use it normally for our immediate needs - but, we lack the value of h, which can be substantiated, by trigonometry. Of course, this only occurs when we don't have the value of h, but do have, or can get the values of, the rest of the triangle.

So, we can utilize trigonometry, to get h, starting with the fact that sin C = h / a. If we multiply both sides by a, then h = sin C x a. And, if we substitute that into the equation for the area of a triangle, as the value of h, then it'd simply be A = 1/2 b x (sin C x a).

This is related to the area formula that we are familiar with, because it is the area formula that we are familiar with - the only thing changed, is that h is a different value. Lastly, these letter can change around a bit, as such:

[Math Is Fun]

Works Cited: Math Is Fun