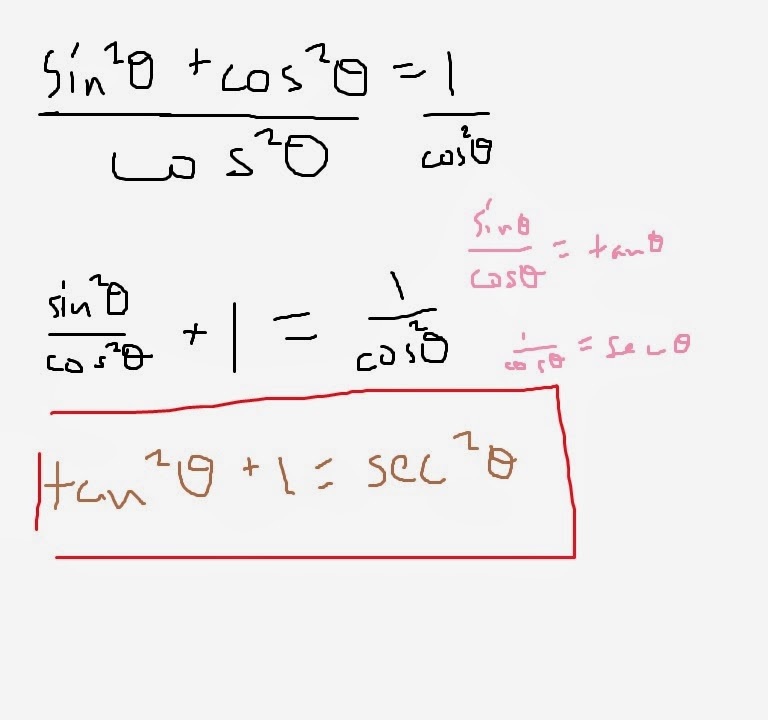BQ #7: Unit V - Derivatives and the Area Problem

The formula for the difference quotient comes from a secant line intersecting twice, through a parabola. As it intersects through a parabola, two points are shared by the two lines. In order to work with tangent lines (lines that touch other lines upon only one point, and which we plot out with derivatives), we want the space between those two lines to be literally 0, meaning ideally, that we want to make them the same.

If we label them exactly as we were told to by a higher entity, then we label the further point as (x+h), and the closer point as just 'x', making the space in between them, 'h'. Their respective y-values, would be f (x+h) and f (x), which basically mean that they are plugged in and calculated into whatever equation we have, to get the y-value. Below is an example of what we have just done.

Somehow, we find it necessary to find the slope of the secant line; so, we utilize the slope formula of (y2 - y1) / (x2 - x1), which, if we plug in the values of our previous graph into, we get ( f (x+h) - f (x) ) / ( (x+h) - x) ) , which simplified, would be (f (x+h) - f (x) / h). And as we all know, that is our formula for the difference quotient, which is inextricably tied to derivatives, somehow.

To make the points (nearly) equal to each other, we can set the limit of h to 0, creating a situation where the points are not equal to each other, but extremely close to one another. After working with the difference quotient, using any sort of equation, we would arrive at an end where the variable 'h' probably exists. By making the limit of h equal to 0, we replace the secant line (two intersections), with the tangent line (one intersection), which are tied to derivatives by the fact that derivatives plot out the slope of every tangent line of any graph. Something like that.

BQ #6: Unit U

1) What is a continuity? What is a discontinuity?

A continuity is when a function proceeds without interruption, meaning that there are no discontinuities. Continuous functions are predictable, and one would be able to draw the function in its entirety without lifting their writing utensil. To extrapolate on my earlier point of "no discontinuities", I meant that the function contains no holes, breaks, or jumps - respectively, a missing point in the graph, a vertical asymptote which invalidates a specific x-value, or a random jump up or down in the function. A continuous function looks like this:

A discontinuity is when a disruption in the continuation of a function occurs. This may occur through either removable discontinuities - holes, or non-removable discontinuities - jumps, oscillating behavior, or unbounded behavior. Holes are when there is a missing point in the graph, jumps are when a graph drops/jumps, oscillating behavior is when there are wiggles, and unbounded behavior is when there is a vertical asymptote. The reason why we separate these into two families, is because removable discontinuities have limits, because their left/right limit values are the same, as we can see in the picture below. Therefore, the non-removable discontinuities must not have limits - due to different left/right limit values, no exact point, or unbounded behavior.

2) What is a limit? When does a limit exist? When does a limit not exist? What is the difference between a limit and a value?

A limit is an intended value of a function. It exists when a function is continuous, or when there is a jump discontinuity (a removable discontinuity). This is because as long as you can trace along the function from both sides and end up at a single, same point on the graph, there is an intended value. It doesn't exist when there is a non-removable discontinuity within the function - namely, jumps, oscillation, or unbounded behavior. This is because you can't end up at a point by tracing from left/right of the point, because of a sudden change in the y-value, no specific coordinate, or a restriction upon a value, respectively. The difference between a limit and a value is that a limit is intended, while the value is what is actually there. In the bottom example, the limit of the function is -2, but the actual value of the function is 2.

3) How do we evaluate limits numerically, graphically, and algebraically?

To evaluate a limit numerically, one would set up a table with values very near the point which you are trying to reach, and what they end up being after you plug them into the function. In the example below, you would reason that whatever is between the values which are very close to the intended point, is between the left/right close values, just as you would with any other numerical evaluation of a limit.

To evaluate a limit graphically, you would simply trace from left/right of the point, in order to find the limit. In the previous example, you would trace left/right of the x-value of 1, and end up ending up at 1 for your limit.

To evaluate a limit algebraically, you would utilize algebra skills in order to find a way in which you can plug in the number which x approaches to get something other than indeterminate form, or infinity of some sort, which are the only two restrictions for evaluating limits algebraically. The very first method in which you would try to evaluate a limit algebraically, would be plugging in the number which x approaches directly into the function. If that results in indeterminate form, or infinity, then you must move on to factoring, which would remedy the issue of indeterminate form. When you can't factor to prevent indeterminate form, you have to multiply by conjugates, usually for radicals, in order to get something other than indeterminate form. Lastly, if you have infinity of some sort, you would have to divide the entire function by the highest power variable in order to somehow fix the problem, and get an answer with substance - without the vagueness of  infinity.

BQ #4: Unit T Concept 3

Why is a "normal" tangent graph uphill, but a "normal" COtangent graph downhill? Use unit circle ratios to explain.

Before we delve into the material, there are two important precursors to the logic that shall be put into explaining just why tangent graphs are typically uphill, while cotangent graphs are typically downhill.

Firstly, it's crucial to know that the ratios for tangent and cotangent, in terms of sine and cosine, are sin/cos, and cos/sin, respectively. From that, we would know that whenever cosine is zero, tangent shall be undefined, resulting in an asymptote, and the same goes for cotangent whenever sine is zero as well.

Secondly, we should know that the x-axis for these graphs is in terms of the unit circle - of π and all that. And, we know that in certain areas of the unit circle, tangent/cotangent are positive/negative. They're both positive in Quadrants I and III, and therefore, are negative in Quadrants II and IV. Since every π/2 on the x-axis is a quadrant, the areas where tangent/cotangent are positive/negative can be organized neatly into certain portions of the x-axis.

Basically, asymptotes divide these portions into repeating portions of either positive to negative (going from left to right), or negative to positive. The reason for which tangent and cotangent differ in where they are allowed to be positive/negative, is that their asymptotes are located in different places - where sine or cosine are zero.

In the above picture, there are asymptotes at π/2 and 3π/2, since that is where cosine is equal to zero. In the sections where tangent is allowed to continually exist for two sections of the graph, it goes from negative to positive, from left to right.

In the above picture, there are asymptotes at π and 2π, since that is where sine is equal to zero. In the sections where cotangent is allowed to continually exist for two sections of the graph, it goes from positive to negative, from left to right.

BQ #3: Unit T Concepts 1-3

How do the graphs of sine and cosine relate to each of the others? Emphasize asymptotes in your response.

Most simply, the graphs of sine and cosine relate to each of the others, in how the others' asymptotes would be where either sine or cosine are equal to zero. This is because sine is the denominator for cosecant and cotangent, and cosine, the denominator for secant and tangent.

Sine is equal to zero, when on the x-axis, it is at zero, and π, as illustrated by the graph below. This is so, because sine is y/r on the unit circle, and therefore, shall only be equal to zero when y is equal to zero. And, y, on the unit circle, is equal to zero, at those places - 0° (zero) and 180° (π). Therefore, there shall be asymptotes for cosecant and cotangent when sine is equal to zero. Asymptotes are important if you want to find out why cotangent goes down. It basically goes down, because the two areas where uninterrupted, consecutive points can continue from left to right, dictate that the left area shall always be positive, and that the right area shall be negative. This is because of the unit circle's ASTC thing. So, since cotangent has to go from positive to negative, it has to go downhill. It's the only way. The only way that I could possibly see sine relating to cosecant, is that they share the same positive/negative areas of the graph. In the areas where sine is positive, cosecant is positive, and vice-versa.

Cotangent is the orange line, and cosecant is the blue line.

Cosine is equal to zero, when on the x-axis, it is at π/2 and 3π/2, as illustrated by the graph below. This is so, because cosine is x/r on the unit circle, and therefore, shall only be equal to zero when x is equal to zero. And, x, on the unit circle, is equal to zero at those places - 90° (π/2) and 270° (3π/2). Therefore, there shall be asymptotes for secant and tangent when cosine is equal to zero. Asymptotes are important if you want to find out why tangent goes up. It basically goes up, because the two areas where interrupted, consecutive points can continue from left to right, dictate that the left area shall always be negative, and that the right area shall always be positive. This is because of the unit circle's ASTC thing. So, since tangent has to go from negative to positive, it has to go downhill. The only way that I could possibly see cosine relating to secant, is that they share the same positive/negative areas of the graph. In the areas where cosine is positive, secant is positive, and vice-versa.

Tangent is the orange line, and secant is the blue line.

BQ #5: Unit T Concepts 1-3

Why do sine and cosine NOT have asymptotes, but the other four trig graphs do? Use unit circle ratios to explain?
Sine and cosine do NOT have asymptotes, because their ratios on the unit circle are x (for cosine) and y (for sine), over r. And, r shall always be equal to 1, being the length of the radius of the circle. The logic behind that explaining how they don't have asymptotes, is that for there to be an asymptote, the denominator of a trigonometric function's ratio, has to be able to be equal to 0. Asymptotes only exist when there is a denominator that could possibly be equal to 0, therefore restricting a certain part of the graph. It is from that same requirement for there to be an asymptote, that we can reason that secant/cosecant/tangent/cotangent have asymptotes. Their ratios on the unit circle should be, respectively: r/x. r/y, y/x, and x/y. Since their denominators are not restricted towards being solely 1 as sine and cosine are, 0 is a possibility for the denominators. The end.

BQ #2: Unit T Intro

How do the trig graphs relate to the unit circle?
Trig graphs relate to the unit circle in how the unit circle can be utilized to find where a certain trig function is positive or negative on a graph. For example, sine is positive in the first and second quadrants - between 0° and 180°, or between 0 and π. If we utilize radians on our x-axis, and have some fraction of π as our markings, then we may isolate the area of the graph between 0 and π as the area in which sine would be positive. Finding these positive/negative areas works with every trigonometric function, though you would have to account for asymptotes as well for denominators that could possibly be equal to 0.

Period? 
Why is the period for sine and cosine 2π, whereas the period for tangent and cotangent is π?
The periods for sine and cosine are 2π because it takes a full rotation of the unit circle, which is 2π, for sine and cosine to fulfill the requirements to be periods. And, a period is a portion of any trig graph that is repeated over and over again without change. To illustrate this example, the values of sine, going through the unit circle's four different quadrants, should be +, +, -, -. Having anything less than those four repeating themselves would create inconsistency, so there you have it. On the other hand, the periods for tangent and cotangent are π because it takes half the rotation of the unit circle. π, for tangent and cotangent to continually repeat themselves consistently. The values of tangent/cotangent, going through the unit circle's four different quadrants, should be +, -, +, -. And having just two repeat themselves continually should be enough to constitute an acceptable pattern.

Amplitude?
How does the fact that sine and cosine have amplitudes of one (and the other trig functions don't have amplitudes) relate to what we know about the Unit Circle?
Sine and cosine have amplitudes, while the other trig functions don't have amplitudes, because their ranges are restricted by how both of their trigonometric ratios have 'r' as the sole value in their denominators. And, on the unit circle, 'r' is equal to 1, being the length of the radius. The other trig functions don't have amplitudes because restrictions such as 'r' aren't in their ratios.

Reflection #1: Unit Q - Verifying Trig Functions

1. Verifying a trigonometric function means simplifying it and or replacing it with other trigonometric functions so that it may equal a set value. You would multiply/divide/add/subtract numbers or some other mathematical asset in order to advance with the equation and simplify it, until it arrives at the value you want it too equal. You may also replace trigonometric functions with other trigonometric functions, such as making tangent into sine divided by cosine. Or, you could make sine squared added with cosine squared, equal 1. One should really try to work with all of the trigonometric identities in order to help them arrive at what they want. And, it will always (at least for what we're doing) be equal. You're not trying to prove it wrong or right - rather, you're showing the work that it takes in order to prove it right. So, if you ever find adversity, don't pass off the equation as invalid.

2. I have found all of the tips and tricks equally helpful. The best tip/trick that I believe anyone could get, is that all of the equations are valid, so you can't give up and write it off as not equal. The most fundamental, and necessary (for about each and every problem you'll have to solve) is tip/trick, is that you have to utilize identities. Unless, of course, you get the problem tangent plus 1 equals tangent plus 2 minus 1, which would then necessitate the question of whether or not you are doing the right problem.

3. Basically, I'd look at what I could do: subtract/multiply by conjugate/replace, and do it. If I end up at a dead end, I'd try again, until I'd get it. And if I don't get it again, I shall try again.

P.S. Not giving up is the fundamental thought process for success in Unit Q.

SP #7: Unit Q Concept 2 - Finding All Trigonometric Functions Using Identities

This SP #7 was made in collaboration with Sergio Sanchez. Please visit the other awesome posts on their blog by going here.

Our given is:

One of the first and foremost steps that must be undertaken, is identifying which quadrant we are working with. Although, using the values of the trig functions and their accompanied signs would do just as well.

Next, we'd just go right into solving this with trigonometric identities. It's pretty self-explanatory had one taken this course. But, for the sake of something: first, I list out the identity, and then, substitute in the value(s) that I already have. I then solve it until there is one unknown trigonometric function is on one side, and a value is on the other.

As for Sergio's work, I suppose that I shall put forth some sort of explanation, in lieu of the original creator, who just gave me this picture. Basically, he plugged in values that were given (from the tangent trigonometric function), into the Pythagorean Theorem, in order to get the excluded side's value. Having gotten all of the sides, he just plugged them into the rest of the unknown trigonometric functions.

It is important that one remembers what all of the trigonometric functions mean - what sides they represent, and how they represent each other. As in, you have to remember that sine is opposite / hypotenuse, and also, 1 / secant. This is important because if you could fail pretty easily if you use the wrong functions/identities. It's also very important for one to remember to rationalize (which I did), and reduce (which I didn't do). Apparently, it's the most important thing you could do for yourself, for forgetting to do so, would result in loss of points on your tests or whatever.

I/D #3: Unit Q - Pythagorean Identities

Inquiry Activity Summary:

1) sin² θ + cos² θ = 1
According to some higher truth, this is true - so, I guess that I'll do as I am told and prove this Pythagorean identity true, in terms of the Pythagorean Theorem and a unit circle. In terms of the unit circle, the Pythagorean Theorem would be x² + y² = r². Since we want 1 on one side, we should divide both sides by r², which would leave us with (x/r)² + (y/r)² = 1. In the unit circle, the ratio of x/r is sine, and the ratio of y/r is cosine. So, if we substitute that in, we get sin² θ + cos² θ = 1.

2) The Two Other Ones
What you would basically do, is divide both sides by either trigonometric function, in order to create ratios that would equal other trigonometric functions. Meaning: you create different ratios by making either sine or cosine equal to 1.

Inquiry Activity Reflection:

1) "The connections I see so far between Units N, O, P, and Q so far are" that they all work together - the unit circle, angles, trigonometric functions, all that stuff - in order to make our experience in math class harder. They all made us critically think about what we are given, and helped us put the pieces of this conundrum together.

2) "If I had to describe trigonometry in THREE words, they would be": "Gotta go fast."

WPP #13/14: Unit P Concepts 6-7 - The Laws of Sine and Cosine

This WPP13-14 was made in collaboration with Sergio Sanchez.  Please visit the other awesome posts on their blog by going here.

Sergio's Problem
Mark arrives at a rather tall building with the rest of his band (to sign a record deal). He is standing 50 feet away from the building, when he looks up, and sees a large He-man banner hanging from one of the windows, and thinks to himself: "Well, would you look at that." If the angle of elevation to the top of the building is N 45° W degrees, and the angle of elevation to the poster is N 25° W degrees, at what height is the banner hung?

[TV Movie Poster]

Our first step in solving this, would be to figure out that the height of the wall is of no relevance - Sergio's fault - yet still, draw a picture of it.

Our next step would be to include the poster and label our given values (50 feet and 25°), and from there, calculate the other angle, since Sergio had decided to simplify our lives and make this a right triangle, which would leave the other angle as 65°.

Lastly, we would utilize the Law of Sines in order to match up 65° with 50, and make sin 65° / 50 equal to sin 25° / x, which, cross-multiplied and simplified, would lead to 23.3 feet as the height of the poster.

Brian's Problem
He-Man smiles upon his admirers, and although he was just a a guy on a poster, his bright smile reflects the sunlight, and shines the radiance upon Mark and the rest of his band. Somehow, he finds that the angle from which He-Man's smile shined light upon his buddies and him, was 115° (navigation method), and that the lengths that had sandwiched that angle, were 35 feet and 25 feet. What length of area did that light cover?


Our first step would be to draw our triangle and label all of the parts, in order to help us organize our next actions.

Our next and last step, would be to plug in all of our values into the Law of Cosines, simplify, and find our answer.

BQ #1: Unit P Concepts 1-5: Non-right Triangle Trigonometry

1. Law of Sines: The Law of Sines is indispensable in sustaining our cushy, privileged lives, because it maintains the space-time continuum in our universe, and because you need it in order to solve for all of the values of any triangle that exists. Of course, you could use the Pythagorean Theorem and other simpler trigonometric functions - but only for right triangles, though, for some apparent reason.

We could prove this law by utilizing our previous knowledge of trigonometry, by creating a line perpendicular to side b and touching the vertex of angle B in a non-right triangle. We shall label this side, h, for the sake of convenience for something else we shall do in just a moment.

Now, we have something that we can work with - two right triangles. And, if we use trigonometry, we will be able to prove the Law of Sines using our prior knowledge. Basically, sine of A, would be h/c, and sine of C, would be h/a. If we multiply both sides of sin A = h/c by c, then h = sin A x c. And if we multiply both sides of sin C = h/a, then h = sin C x a.

With h being equal and all, we will be able to set them equal to each other. This makes sin A x c = sin C x a. If we divide both sides by c x a, then sin A / a = sin C / c, which proves the Law of Sines (or at least 2/3 of it). Just kidding. Since we only use two at a time (you couldn't possibly have = twice in an equation, right?), all we would have to do is switch around the letters, and everything would be fine.

4. Area of An Oblique Triangle: The area of any triangle should be 1/2 b x h (b is base, which would be the side of b anyways, and A, area in this case), which roughly translates to: half of double of the triangle. We would use it normally for our immediate needs - but, we lack the value of h, which can be substantiated, by trigonometry. Of course, this only occurs when we don't have the value of h, but do have, or can get the values of, the rest of the triangle.

So, we can utilize trigonometry, to get h, starting with the fact that sin C = h / a. If we multiply both sides by a, then h = sin C x a. And, if we substitute that into the equation for the area of a triangle, as the value of h, then it'd simply be A = 1/2 b x (sin C x a).

This is related to the area formula that we are familiar with, because it is the area formula that we are familiar with - the only thing changed, is that h is a different value. Lastly, these letter can change around a bit, as such:

[Math Is Fun]

Works Cited: Math Is Fun

WPP #12: Unit O Concept 10 - Angles of Elevation and Depression

[cdn.screenrant.com/wp-content/uploads/He-Man-Masters-of-the-Universe-Movie.jpeg]

He-Man and his comrades are heading towards the battlefield, in a planned face-off against Skeletor and his goons. When they confronted their enemies, they had found an unfortunate situation: Skeletor's forces were on higher ground than them (on a mountain), leading to a widely unfair advantage. He-Man thought out the situation while his comrades kept the enemy busy, and had decided to calculate whether or not throwing a projectile at Skeletor was practical or not. He had estimated about 200 feet of distance between them (from He-Man to the base of the mountain), and a 70° angle of elevation to Skeletor. How far would his throw have to be, in order for his projectile to (diagonally and in a straight line) reach Skeletor?

  S(keletor)

   |\

   |  \

   |    \                                  cos 70° = 200 ft.

   |      \                                                    h

   |        \

   |          \                                  h x cos 70° = 200 ft.

   |            \

   |              \                                     200 ft.

   |                \                                  --------- = 584.76 ft.

   |                  \                                cos 70°

   |             70° \ H(e-Man)

         200 ft.

Seeing as how a throw that would have to travel 584.76 ft. was impractical, He-Man had simply decided to find a nearby mountain with a higher elevation, in order to reduce the required power in that throw. After a short while, He-Man finds a fitting spot upon a mountain, measuring 600 ft. in height. If Skeletor's elevation was 549.5 ft., and the angle of depression was 10°, then what would be the distance that He-Man's new-and-improved throw have to be?

I/D #2: Unit O - How Can We Derive the Patterns For Our Special Right Triangles?

1) We may derive a 30/60/90 degree triangle's special pattern from an equilateral triangle with a side length of 1, by first dividing the triangle into two halves that are completely equal. You'd split it right in the middle, creating two triangles that share one side of the previously whole equilateral triangle (which equaled 1), and the side that was created by splitting them in half. They each have their own side of 1, across from the 90° angle that they both have, which was created by the division.

Since we divided the side which had previously equaled 1 into two equal parts, then each triangle must have a side of 1/2. So, if we proceed with that deduction, then that side, squared, added with the other side that's not the hypotenuse, squared, should equal the hypotenuse, squared. Basically, a² + b² = c² (Pythagorean Theorem), with 1/2 being a, the other leg being b, and 1 being c. This works because the triangles we had created, have 90° angles, and therefore, have an assumed hypotenuse across from them, along with the values for a and b that fit into the aforementioned equation. (1/2)² + b² = (1)² would be 1/4 + b² = 1, and subtracting 1/4 from both sides would result in 3/4 as the value for b². And, if we take the square root of the entire fraction, then it should equal √3/√4, which would reduce into √3/2.

Lastly, we'd have to save this extremely rare knowledge, by multiplying everything by 2, and then, by a variable, so that this pattern will be easily transferable to any 30/60/90 degree triangle. Multiplying each side by 2n, basically, would yield a hypotenuse of 2n, a value of n for the side across from the 30° angle, and a value of n√3 for the side across from the 60° angle. This pattern shall forever exist for any 30/60/90 degree triangle, since the pattern was derived from ratios that will be the same for all 30/60/90 degree triangles.

2) We may derive a 45/45/90 degree triangle's special pattern from a square with the equal sides of 1, by diagonally dividing two 90° angles (across from each other) exactly in half, and making four 45° angles - two for each triangle. Each triangle would then, each have two sides that equal 1, and share a hypotenuse.

So, since the two triangles that we have given life to have 90° angles, then the Pythagorean Theorem can be utilized in order to find the length of the hypotenuse in this set-up. 1² + 1² = c² shall become c² = 2, and from that point onward, be √2.

In order to again, preserve our newly-discovered and revolutionary (in the field of mathematics) pattern, we must multiply all of our triangles' values by n, in order to create a distinct pattern that we can follow for any 45/45/90° triangle. Everything just basically gets an n attached to it.

Inquiry Activity Reflection
1) Something I never noticed before about special right triangles is that their established patterns can be deduced from a logical procedure, instead of just being "there", because we were told that it happened to be "there".

2) Being able to derive these patterns myself aids in my learning because I'm not just remembering given facts or something - I'm actually finding out this stuff myself.

I/D #1: Unit N Concept 7 - How Do Special Right Triangles and the Unit Circle Relate?

Inquiry Activity Summary
1) The first and foremost part of interpreting a 30° special right triangle, is setting the side opposite of the 30° angle to x, and going along with that, the hypotenuse as 2x, and the other leg of the triangle as x√3. In order to align this set-up with the unit circle, we must set the hypotenuse equal to 1, since the radius of a unit circle will always be 1, and the hypotenuse will be exactly between the Unit Circle's center and its arc. So, if we set the hypotenuse to 1, then we basically divide all of our previously-acquired values by 2x, making it proportionate to the 2x = 1 ratio that we had fabricated. So, the x would become 1/2, and the x√3 would become √3/2.

2) In order to make sense of a 45° special right triangle, we should first set up the hypotenuse as x√2, and the other two sides as x (since both sides are the identical, according to geometry). To match this up with the unit circle, we set the hypotenuse to 1, which is most simply done, by dividing x√2 by x√2, which gives us 1. Dividing x by x√2 would make x times (1 / x√2), creating a situation in which the x's cancel out, and you are left with 1/√2. In order to rationalize that, you would multiply it by (√2 / √2), which would result in (√2 / 2) for your two other sides.

3) Lastly, the 60° special right triangle should include the exact same values as the 30° special right triangle would. All that one would have to do, is ensure that values accordingly match up with degrees. But, I suppose that I have enough time to explain this. Basically, the side opposite of your 60° angle would be set to x√3, your hypotenuse set to 2x, and your other leg, set to x. In order to substantiate a hypotenuse equal to 1, you would divide all of the values by 2x, and end up with 1 for the hypotenuse, √3/2 for the side that had previously equaled x√3, and 1/2 for the side that had previously been x.

4) How Does This Activity Help You To Derive The Unit Circle?
I suppose that this activity helped me more easily identify all of the values that encompass various common degrees in a unit circle, by listing out all of the possible values that I should know. If I were tasked to find out the coordinates of wherever any 30° or 60° angle's terminal side met with the Unit Circle's arc, there could only ever be three values that I need to know (their signs and or order depend upon which quadrant of the circle they are in): 1, √3/2, and 1/2. For the 45° angle, literally the only two values I would ever need to figure out coordinates of wherever the 45° angle's terminal side met with the unit circle's arc would be 1 and √2 / 2. This stuff is really useful in trigonometry and all.

5) The triangles drawn in this activity were in Quadrant I, ergo, their positive coordinates. The signs would change in differing quadrants, with Quadrant II implying a negative x-coordinate, Quadrant III, a negative x-coordinate and y-coordinate, and Quadrant IV, a negative y-coordinate.

Inquiry Activity Reflection
1) The coolest thing I learned from this activity was that from remembering three simple values (√3/2, 1/2, and √2 / 2), you can get everything that you need in the Unit Circle. All you'd have to do is remember what different quadrants do to the signs of the values, and all that other stuff.

2) This activity will help me in this unit because I can now, more easily remember the Unit Circle.

3) Something I never realized before special right triangles and the unit circle is that just by identifying which side is the longest of the two of a 30° or 60° angle, you can determine which has the √3/2, and which is the 1/2 (√3/2 is bigger than 1/2).

RWA #1: Unit M Concepts 4-6 - Conic Sections In Real Life

Parabola

1) Definition: The set of all points equidistant from a given point, known as the focus and a line, known as the directrix.

2) Algebraically: The algebraic equation that is used to standardize parabolas is as follows: (x-h)^2 = 4p(y-k) or (y-k)^2 = 4p(x-h). Basically, one would modify any given equation that is determined to be one of a parabola into this format, most usually, through completing the square. In order to distinguish equations of parabolas from equations from other conic sections, you basically need to know only one thing: one variable is square, while the other isn't. This is a distinct feature of the parabola that we don't find occurring within equations for circles, ellipses, or hyperbolas. Anyways, by looking at the value of p, and at which variable is squared, you may determine what the parabola would look like graphically, as in its orientation and all. 

Graphically: The first and foremost characteristic that one would find while examining the parabola, is that it looks awfully similar to the letter 'U'. Its orientation can be determined through the sign that is complementary with the value of p, and the variable that holds the square. If x is squared, then the parabola will either face up or down - up if the p is positive, and down if it is negative. If y is squared, then the parabola will either face right or left - right if the p is positive, and left if the p is negative. The point at which the parabola can be directly divided in half - that is, also considered its vertex - will be known as the vertex, and the line which divides it exactly in half, known as the line of symmetry. The focus point, which will be on the line of symmetry the distance of 'p' away from the center, will help one decide what the orientation of the graph is like - by way of being in the direction of the lines. Lastly, the focus point may also determine whether the parabola is fat or skinny - if it is close to the vertex, then it will be skinny; if it is far away from the vertex, it will be fat. AND the directrix is basically the opposite of the focus point, and is a line.

 
http://www.mathsisfun.com/geometry/images/parabola-formula.gif

Features Of: The vertex is most basically, (h,k), the focus, (h+-p,k) or (h,k+-p), depending on which variable has the square and what the value of p is, the line of symmetry, either h or k, again, depending on which value has the square, and p is the variable that precedes the variable without the square, divided by 4. Ah, and the directrix is the exact same thing as the focus point - save that it is determined by subtracting p if the focus is found through addition, and vice-versa - and, it is a line.

3) Real World Application: As demonstrated in the video below, there are many instances in real life in which parabolas occur. For example, when the teenager shoots the basketball into the basketball hoop, a parabola is seen - and even outlined, too. If it were practical, I suppose that basketball players would study up a bit more in math, in order to improve their shots.



4) Works Cited: http://mathworld.wolfram.com/Parabola.html
http://www.mathsisfun.com/geometry/images/parabola-formula.gif
https://www.youtube.com/watch?v=FXuTKpp-vME

WPP #10: Unit L Concepts 9-14 - Probability

Create your own Playlist on LessonPaths!